Generally when an astronomer is analyzing a part of a sky, they need the complete picture. When I say complete picture, I mean all kinds of data: radio wavelengths , visible wavelengths, x ray data etc . Different kinds of data is gathered using different telescopes (specific to the wavelengths).
So imagine, you have one set of data with tells you about the radio wavelengths of different sources, another of visible wavelengths. To get a complete picture, you need to map objects from data/catalog 1 to objects of data/catalog 2.
For simplicity, lets assume catalogs contain some common information.
for now (RA and DEC in degrees). It may be possible that the same object's coordinates differ by a small value in different catalogs, so you cannot just directly match by values of the coordinates. What we would do is, take every object in catalog 1 and find the object in catalog2 which is closest to it. By closest, we mean, you find the distance between those two coordinates and and check for which object this distance is least.
But then, some objects may not be in some catalogs, for example. an object which only radiates lets say radio wavelengths would not be available in the visible spectrum catalog. We might therefore match a wrong object. To correct this, we can keep a minimum agreed upon distance which is needed for assuming that the objects are actually the same object in space.
To give you a picture where this is used, lets say we are looking for AGN or
, which in a sentence is a compact region in middle of galaxies emitting energy in a variety of wavebands.There is a theory which says these are powered by massive blackholes (the accretion discs of these blackholes). So looking for them will also help in looking for blackholes, which are generally hard to find.
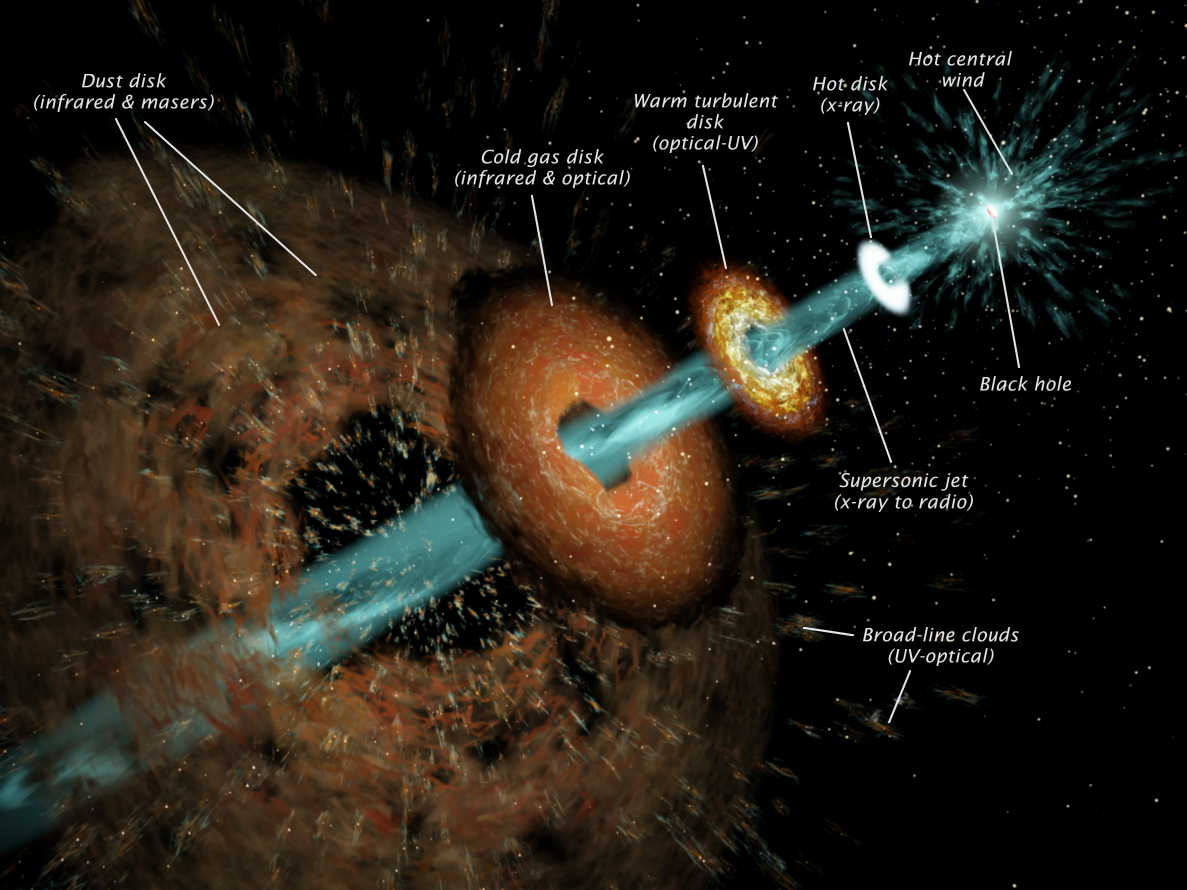
If we find an object and successfully match objects in different catalogs, we get a complete picture of the object which can then be studied in more depth to find its characteristics.
Now, matching seems fairly simple, you take an object , get distance of this object from every object in the second catalog and the object which has the min distance and falls within the min agreed upon distance is you object. But the catalog doesn't contain data for one or two object, not even hundred object, it contains data for thousands and thousands of objects.
(When i was studying this, i was trying to find catalog to check efficiency of my implementation of the algorithm , i encountered catalogs of sizes 7GB!!)
So the naive approach is looking (from a developer's point of view) is two "for" loops on the catalogs, so your complexity is O(n^2). To match catalogs with thousands of data, this would require days. Clearly not efficient!.
Now that you know about them, the algorithm is easy. Here we are assuming that we have all the data for the catalog, not new data points aren't coming in a stream for example. It is one static data. To search efficiently, we make a kd tree using one of the catalog and then search the objects from other catalogs using this kd trees. This is much efficient since to search for one object , the worst case is you traverse every node of the tree, which will lead to the worst complexity being O(n^2) as opposed to the naive algorithm which was O(n^2) in all cases. We can find a object in the kd tree in O(log n) , assuming the tree is balanced.
, a famous python library for astronomy has optimized this algorithm even more to match large data in a relatively very short duration of time. One can use their "match_to_catalog_sky" function to crossmatch catalogs.
The application of KD tree, doesn't stop just here, you can modify the algorithm to get more than 1 nearest neighbors. Nearest neighbor problems are themselves applicable in a variety of pattern searching, so one can use the tree there too.
