Skip to content
 K-D Trees
K-D Trees
K-D Trees are basically a generalization of binary search trees, where you can store n dimensional data. These need not only be cartesian plan points, but can be for example bio-metric, storing DNA information for example. But every node in that tree should be of same dimension.
Intuition
Imagine the x axis. Only x-axis, you have no there axis' or dimensions available for now. So basically a number line.
<------------------------------- -4 -3 -2 -1 0 1 2 3 4 5 6 7------------------------------------------>
If you use a binary search tree, it would visually , directly fall on this line. We made a partition on some x= constant (here x= 0) to make the root.
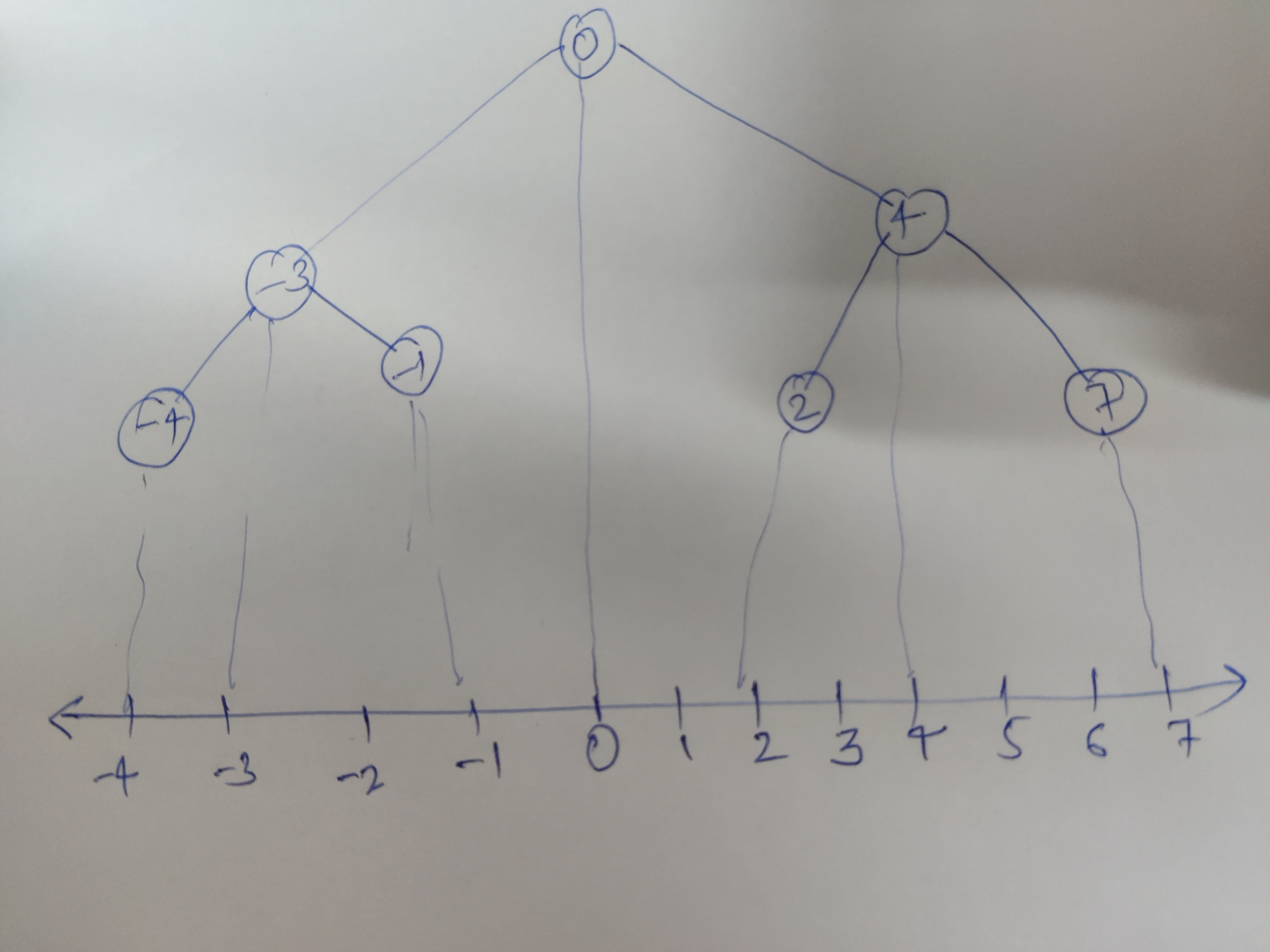

Values having value less than root, lie on the left sub tree and more than the root lie on right subtree.
Increasing the dimension by one, we are basically introducing a line partition => x = c or y = c. (If another dimension is added, we are introducing a plane partition)
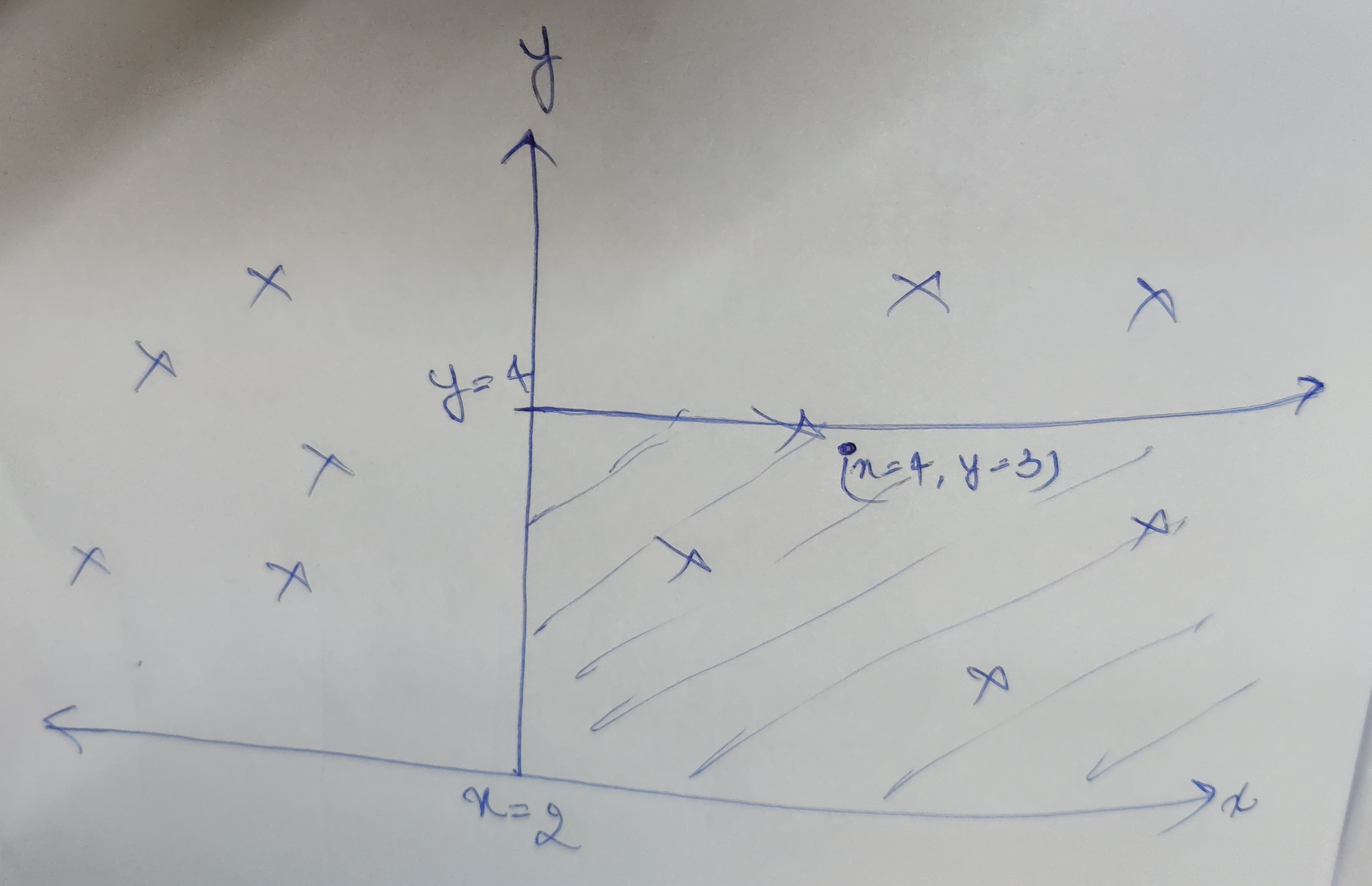

In the above example, the first partition is at x = 2. Now we have two subtrees to make. Points having x less than 2 will lie in left subtree and x greater than 2 will lie on right subtree. Let say we are now making the right subtree, this time the partition will be perpendicular to y axis (need to make a partition on x=2 plane). So we take the middle point having say y=4 and make a partition there (This point becomes root of our right subtree). Similarly we keep on doing this until all points are added in the tree.
We are therefore partitioning a 2D space here.
(Although you can partition n dimensions, kd trees are not efficient after 3 dimension, one can deep dive there using the web :D)
Finding a point in space partitioned.
Lets say (take the example from above), we need to find the point , or find the point closest to x=4, y=3. First we check the x axis partition, we see x=4, greater than 2 so the point should lie in the right subtree. Then in the next iteration to check for alternate axis, y, here y=3, less than our node of y=4, so the point should lie in left subtree now (the right bottom shaded area), in the next iteration, one would check x axis again and move deeper in the tree. So we basically eliminated half of the points in one iteration.
How does one prove that the elimination is correct. Would this fail in some scenario ?
Lets imagine, that we have a Test point (T), for which we need to find a nearest point (this test point is not in the kd tree, its a new point for which we need to check the nearest point in existing data. So your existing data goes in the kd tree, and you compare the new point in the kd tree nodes.) And you have an assumption for closest point (A). How do we prove that eliminating the right half of the partition is correct?
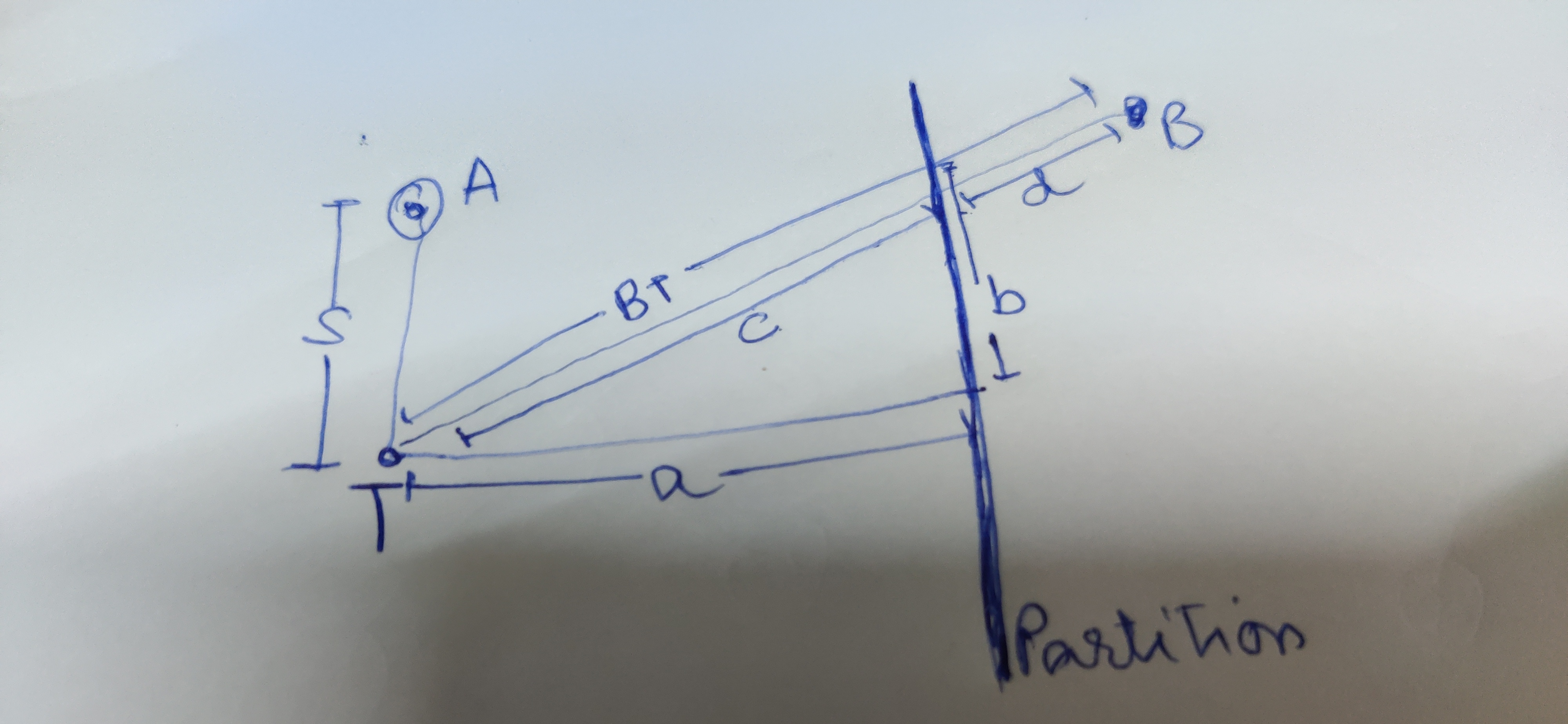

Take a point in the right half, B., all we have to prove now is the distance TB > AT. Visually it is easy to say this, but we need to prove this mathematically to use induction to prove it for n points in the right half. We know OT > AT
BT=c+d=sqrt(a2+b2)+dBT = c +d = sqrt(a^2 + b^2) + dBT=c+d=sqrt(a2+b2)+d
c+d>=sqrt(a2)+d>=a+d>=a c + d > = sqrt(a^2) +d >= a+d >= ac+d>=sqrt(a2)+d>=a+d>=a
AT<OT==>AT<c+dAT < OT ==> AT < c+dAT<OT==>AT<c+d
When would this go wrong?
If a point is very near to the boundary, we might wrongly eliminate the point for being in the other half. Imagine a circle (or sphere, in 3 dimensions) with radius of distance of our current guess. if any other point lies within this circle then it would be the closes point instead. A point would exist if a partition exists. How we do know a partition intersects our circle ?
We check the distance, if our distance to the partition is less than the radius of the circle then definitely we should check that subtree before eliminating it. This is also depth first search , we would go explore the modes in depth and on returning, we check if the distance of this axis is less than our best uptil now and if it is we would go in the other subtree to explore it.
Implementation
Although the algorithm and the data structure itself may sound complicated, the implementation isn't so.
Creating a kd tree
To alternate between axis, as you go deeper in tree, depth % k (dimensions) would give you round robin axis.
axis = depth % noOfDimensions;
The second point to note here is , to make a root node, we need the middle/median point along that axis. We will use the sorted function of python to get that:
sorted(pointList, key = lambda point:point[axis])
class Node():
def __init__(self, val, left, right):
self.val = val
self.right = right;
self.left = left;
class KDTree():
def __init__(self, pointList):
def build(pointList, depth, noOfDimensions):
if pointList is None or len(pointList) <= 0 :
return None;
axis = depth % noOfDimensions;
pointList = sorted(pointList, key = lambda point:point[axis])
median = math.floor(len(pointList)/2);
#print("median", median)
node = Node(val = pointList[median],
left = build(pointList[0:median],depth+1, noOfDimensions),
right = build(pointList[median+1:], depth+1, noOfDimensions));
return node;
self.root = build(pointList, 0, len(pointList[0]));
def contructTree(points):
tree = KDTree(points);
return tree;
Nearest neighbor algorithm
Nearest neighbor calculation may differ based on your use case, for mine, i need to get the angular distance to the point, and compare these distances to check which point is closer (which distance is lesser). But the rest of the code would fairly remain the same.
def getClosestPoint(point, root, depth, k) :
if root is None :
return None;
axis = depth % k;
subtree = None;
oppositeSubtree = None;
if(point[axis] < root.val[axis]) :
subtree = root.left;
oppositeSubtree = root.right;
else :
subtree = root.right;
oppositeSubtree = root.left;
best = compareAndGetClosesPoint(point,
getClosestPoint(
point,
subtree, depth+1,
k), root.val);
bestDistance = getDistance(point, best);
distanceToWall = abs(point[axis] - root.val[axis]);
#print("best till now:", best, bestDistance, distanceToWall)
if ( bestDistance > distanceToWall):
best = compareAndGetClosesPoint(point,
getClosestPoint(
point,
oppositeSubtree, depth+1,
k), best);
return best;
The compareAndGetClosestPoint is a simple helper function:
def getDistance (p1, p2) : #angular dist
ra1, dec1 = p1
ra2, dec2 = p2
b = np.cos(dec1)*np.cos(dec2)*np.sin(np.abs(ra1 - ra2)/2)**2
a= np.sin(np.abs(dec1 - dec2)/2)**2
d = 2*np.arcsin(np.sqrt(a + b))
return np.degrees(d);
def compareAndGetClosesPoint (point, p1, p2) :
if p1 is None :
return p2;
if p2 is None :
return p1;
d1 = getDistance(point, p1);
d2 = getDistance(point, p2);
if (d1 <= d2):
return p1;
else :
return p2;
Check file "kdTree.py" in the git repo: . There is a wrapper function which loads the catalogs, calls contructTree function of KD Tree on one of the catalogs, and runs the other catalog to search each object. The code returns a matches array which contains a point and its closest point coordinates, a set of noMatches array giving a list of points which didnt match.
Want to print your doc?
This is not the way.
This is not the way.

Try clicking the ··· in the right corner or using a keyboard shortcut (
CtrlP
) instead.