Skip to content
Share
Explore
GNN Examples
Mental Action
GNN ~ Sandved-Smith Mental Action
GNN Section
SS Figure1
SS Figure2
SS Figure3
SS Figure4
Mental Action Part3
1
Image from paper
2
GNN version and flags
3
Model name
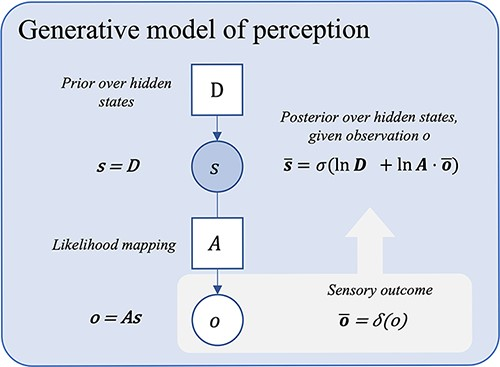
Sandved-Smith Figure 1 #
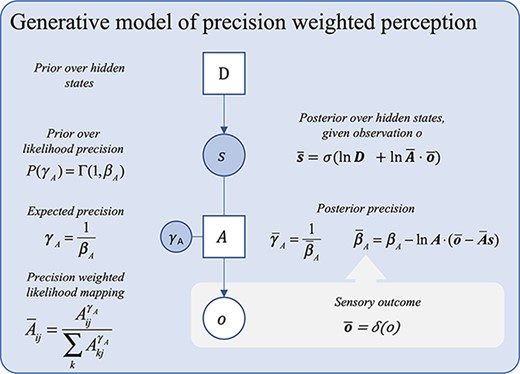
Sandved-Smith Figure 2 #
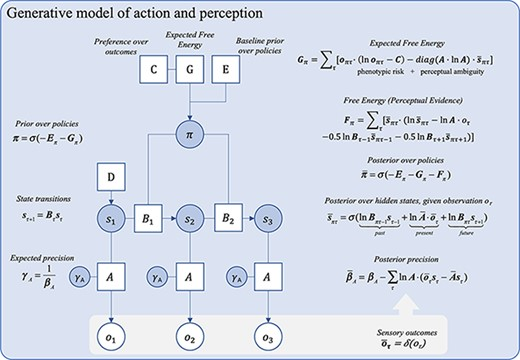
Sandved-Smith Figure 3 #
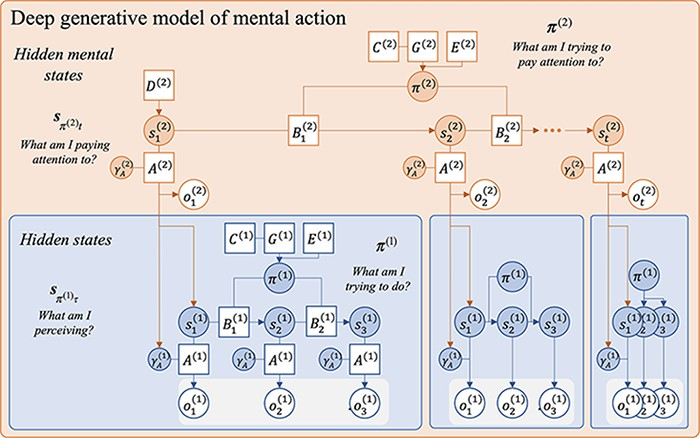
Sandved-Smith Mental Action Figure 3 BLUE and ORANGE #
Sandved-Smith Mental Action BLUE ORANGE GREEN #
4
Model annotation
Static
Perception
This model relates a single hidden state, to a single observable modality.
“A probabilistic graphical model showing a basic generative model for moment-to-moment perception. ”
Static
Perception
This model relates a single hidden state, to a single observable modality.
Compared with Figure 1, there is the introduction of gamma_A as a Precision term.
“A Bayes graph showing a basic generative model of perception with precision.”
Dynamic
Perception
Action
This model relates a single hidden state, to a single observable modality.
“A Bayes graph showing a deep generative model for policy selection.”
5
State space block
A[]
D[]
s[]
o[]
A[]
D[]
s[]
o[]
γ_A
A[]
B[]
C[]
D[]
E[]
G[]
s[]
o[]
γ_A[1]
6
Connections
D<>s
s<>A
A<>o
D<>s
s<>A
A<>o
A<>γ_A
7
Initial parameterization
None
None
8
Equations
s = D
o = As
s_bar = σ(ln(D)+ln(A)*o_bar)
o_bar = δ(o)
Equations
P(gamma_A)=Gamma(1,beta_A)
gamma_A=1/beta_A
A^{bar}{ij}=A^{gamma_A}{ij}/(sum_k(A^{gamma_A}_{kj}))
s^{bar}=sigma(lnD+ln(A^{bar} \dot o^{bar}))
gamma^{bar}_A=1/beta^{bar}_A
beta^{bar}_A=beta_A - ln(A) \dot (o^{bar}-A^{bar}*s)
o^{bar}=delta(o)
Equations
pi=sigma(-E_pi-G_pi)
s_{t+1}=B_t*s_t
gamma_A=1/beta_A
G_pi=sum_t[o_{pi, t} \dot (ln(o_{pi, t})-C)-diag(A \dot lnA) \dot s^{bar}_{pi, t}]
F_pi=sum_t[s^{bar}{pi, t} \dot (ln{s^{bar}{pi, t})-ln(A) \dot o_t - 0.5 * ln(B_{t-1}*s^{bar}{pi, t-1})-0.5 * ln(B{t+1}*s^{bar}_{pi, t+1})]
pi^{bar}=sigma(-E_pi-G_pi-F_pi)
s^{bar}{pi,t}=sigma(ln(B{pi, t-1}s_{t-1})+ln(A^{bar} \dot o^{bar}t)+ln(B{pi, t}*s_{t+1}))
beta^{bar}_A=beta_A - sum_t(ln(A) \dot (o^{bar}_t*s_t-A^{bar}*s_t))
o^{bar}_t=delta(o_t)
9
Time
None
None
10
ActInf Ontology annotation
A=RecognitionMatrix
D=Prior
s=HiddenState
o=Observation
A=RecognitionMatrix
D=Prior
s=HiddenState
o=Observation
γ_A=Precision
11
Footer
12
Signature
There are no rows in this table
Want to print your doc?
This is not the way.
This is not the way.
Try clicking the ⋯ next to your doc name or using a keyboard shortcut (
CtrlP
) instead.