2020

Median Image Stacking
Median Image Stacking

We will now implement binapprox algorithm in 2D matrices. (Refer to BinApprox article for steps)

‌

Step 1: Running mean and std deviation calculations (Using

Welford's online algorithm⁠

)

def calcMeanStdDev (imageArr):

mean = 0

count = 0

m2 = 0

for fname in imageArr :

data = load_fits(fname);

mat = np.array(data)

count += 1

delta = mat - mean;

mean += delta/count;

delta2 = mat - mean;

m2 += delta*delta2;

variance = m2/(count-1)

stdDev = np.sqrt(variance);

return mean, stdDev;

‌

Note this contains the loading of files, each file is loaded once and closed (load function mentioned in Mean Image Stacking article).

‌

⁠

‌

Step 2: Form B bins across [mean-stddev, mean+stddev], mapping each data point to the bin

def binFunc (data, bins, mean, std, binWidth, leftBin):

m,n = data.shape;

for i in range(m):

for j in range(n):

p_mean = mean[i,j];

p_std = std[i,j];

p_bin_w = binWidth[i][j]

p_data = data[i][j];

if p_data < p_mean - p_std :

leftBin[i,j] +=1;

if(p_data >= p_mean - p_std and p_data < p_mean + p_std) :

index = int((p_data-(p_mean-p_std))/p_bin_w)

bins[i, j,index] +=1

return bins, leftBin;

def median_bins_fits(imageArr, noOfBins):

mean, stdDev = calcMeanStdDev(imageArr);

# minVal = mean - stdDev;

# maxVal = mean + stdDev;

binWidth = (2*stdDev)/noOfBins;

firstImage = load_fits(imageArr[0])

leftbin = np.zeros_like(firstImage)

m,n = leftbin.shape;

binsMat = np.zeros((m,n,noOfBins));

for fname in imageArr :

data = load_fits(fname);

mat = np.array(data);

print("image i:", fname)

binsMat, leftbin = binFunc(data, binsMat, mean, stdDev,binWidth, leftbin)

return mean, stdDev, leftbin, binsMat

‌

I commented out minVal and maxVal which i previously used instead of p_mean - p_std calculations. I used

memory profiler library to check the memory consumption⁠

. By removing those variables ( some other variables too that i used ) and directly using the values, I could reduce around 20Mb (I had too many variables).

‌

⁠

‌

Step 3,4: Find the bin that contains the median and return the midpoint.

def median_approx_fits (imageArray, noOfBins):

mean, std, left_bin, bins = median_bins_fits(imageArray, noOfBins);

m,n = mean.shape;

imageCount = len(imageArray);

mid = (imageCount + 1)/2;

median = np.zeros((m,n));

bin_width = (2 *std)/noOfBins;

for i in range(m):

for j in range(n):

count = left_bin[i,j]

for b, bincount in enumerate(bins[i, j]):

count += bincount

if count >= mid:

break

median[i, j] = mean[i, j] - std[i, j] + bin_width[i, j]*(b + 0.5)

#print(median)

return median;

‌

_____________________________________________________________________________________________

‌

More the number of bins, better the median approximate. Plotting the "median" matrix using our plot function (mentioned in Mean Image Stacking).

‌

Using it on the Crab nebula image:

‌

No of Bins = 4

⁠

‌

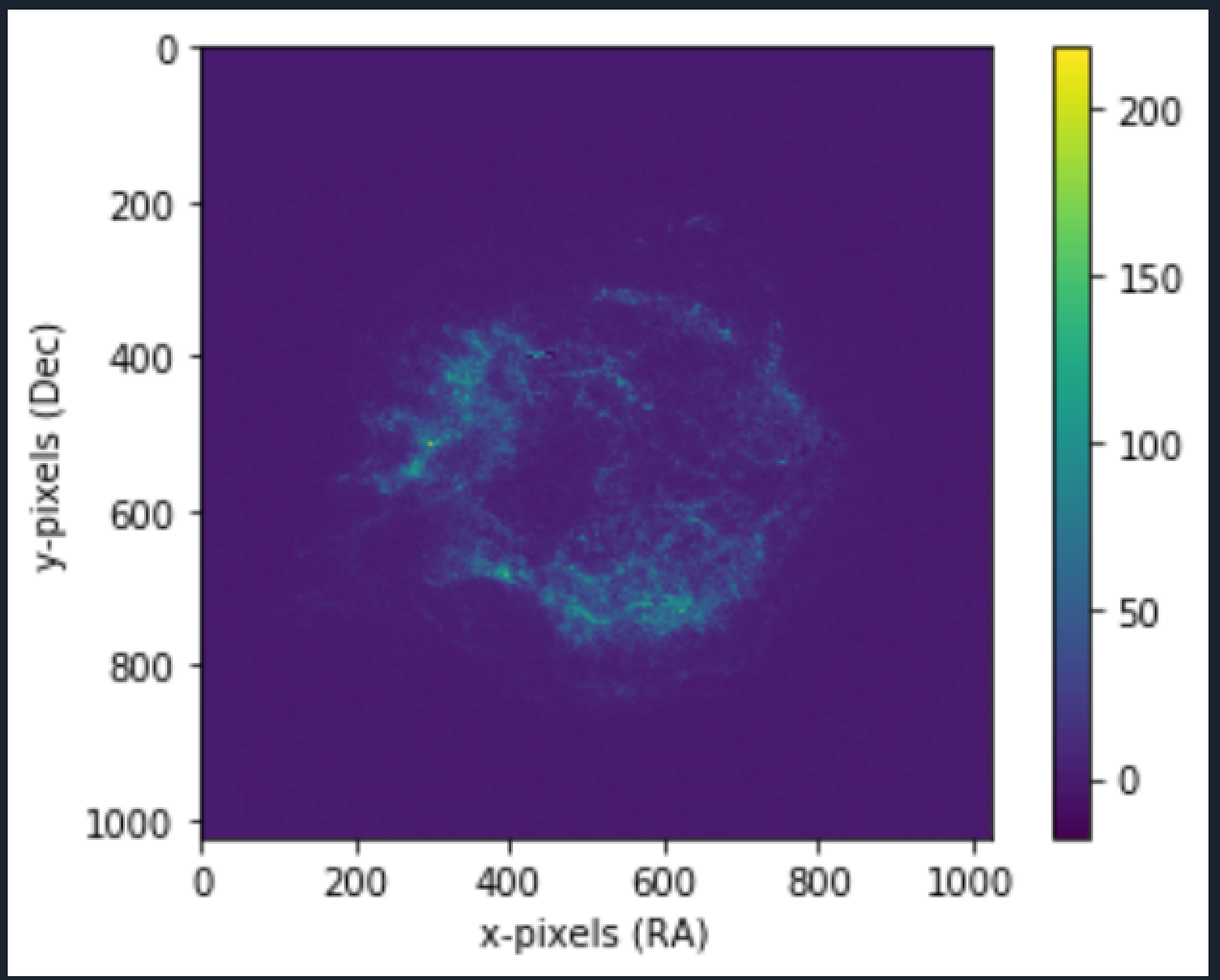
2. No of Bins = 50

⁠

‌

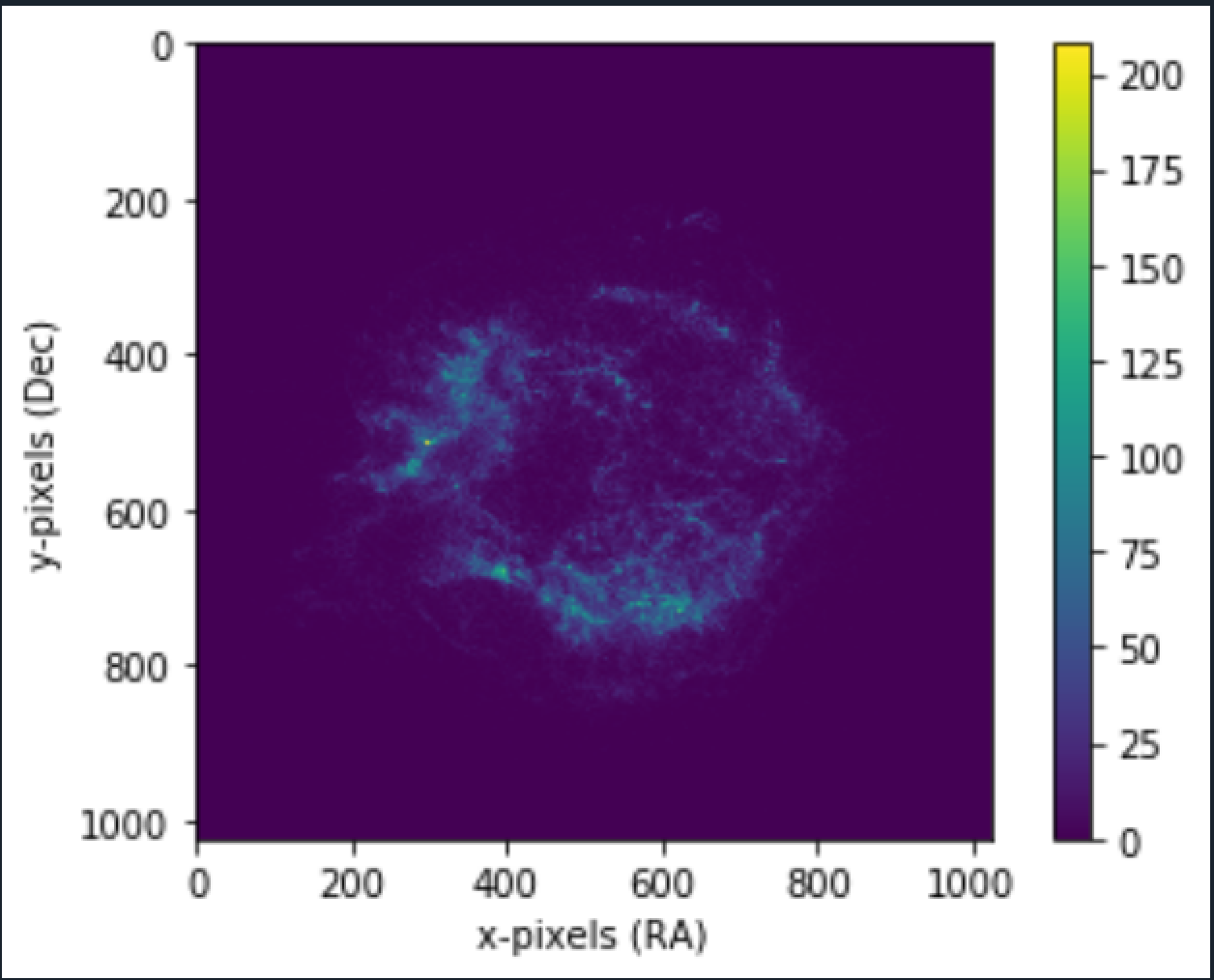
3. Bins: 150

⁠

‌

As number of bins increase, the brighter objects are more visible clearly, like in the left part of the image, we can see a very bright object at around RA = 250, Dec = 500 (Approx). Typically astronomers use no of bins to be around 1000 and use hundreds of images. They also optimize further by parallelizing calculations further.

‌

(Found some fits a part of Data Driven Astronomy Online Course by The University of Sydney)

Want to print your doc?
This is not the way.

Try clicking the ⋯ next to your doc name or using a keyboard shortcut (

CtrlP

) instead.

Median Image StackingMedian Image Stacking

Median Image Stacking
Median Image Stacking