Explore

Lacan, Fractal Memory, & Cellular Automata

@dinodelaomx

Abstract

This article will serve as an introduction to the concept of “fractal memory” in Lacan’s work and explore its applications for cellular automata (CA). The article takes a multidisciplinary approach, bridging areas in computer algorithms, cybernetics, generative art, history, linguistics, philosophy, and psychoanalysis.

Lacan on Cybernetics

Jaques Lacan was a French psychoanalyst best known for his theories on language and symbolic systems. The wide breadth and depth of Lacan’s work far exceed the scope of this article. Instead, this article will focus on Lacan’s teachings on cybernetics which were influential to his earlier work between the months of November 1954 and June 1955. During this time, Lacan held 23 live seminars at the Sainte-Anne Hospital Center in Paris, 5 of which addressed his views on cybernetics. Despite the small fraction of attention that the topic gets when you consider his entire academic work, his last seminar during this period, “Psychoanalysis and Cybernetics, or on the Nature of Language,” marked the significance of cybernetics to Lacanian psychoanalysis.

Why cybernetics? Lacan became interested in how circuits “communicate” through elementary binary code, how machines “think”, and what this has to say about language. Ultimately, Lacan established his own theory of language, demonstrating how cybernetics and elementary ciphering precedes the construction of any formal language. “In other words, within this perspective, syntax exists before semantics. Cybernetics is a science of syntax ...” (Lacan 1955, p. 305)

To demonstrate this ciphering, in The Purloined Letter, Lacan introduces a game of even and odd. The idea is simple: you flip a coin. If its heads – mark even, tails – mark odd. Each toss can be followed by a consecutive toss, constituting an array of tosses. For the purpose of the thought experiment, our perfect sequence of tosses assumes two basic premises:

Each side of the toss has a 50/50 chance of winning.

Each flip is independent of the rest.

Assuming a fair toss, one can generate a sequence of random tosses. Moving forward, black squares are used for “Heads” and white squares for “Tails”.

⁠

If you take multiple groups of three tosses, regardless of their makeup, you will notice that only eight combinations are possible. Lacan assigns each of these eight combinations to a corresponding type.

⁠

⁠

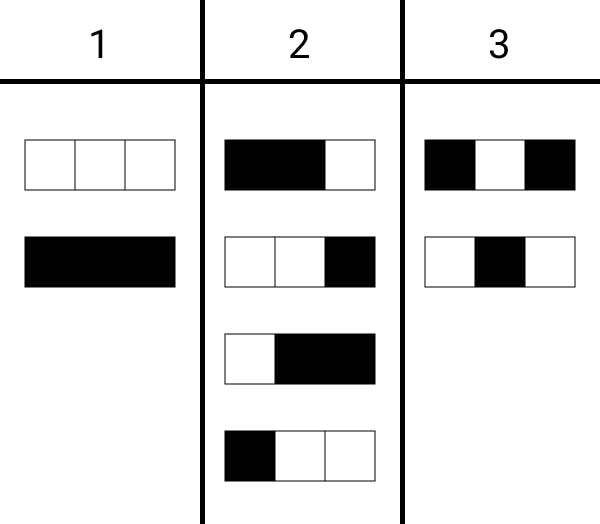
There are different ways one could have categorized these eight combinations. But, Lacan’s division carries an intuitive appeal. For him, Type 1 combinations display symmetry of constancy, Type 3 combinations display symmetry of alternation, and Type 2 combinations display dissymmetry.

It’s also worth noting that similar connections were made three thousand years ago in the koua (often called bagua), or the eight trigrams from the ancient Chinese text, the I Ching. (Liu 2020, p. 309)

⁠

The koua uses continuous and broken lines in its diagram. However, we see a similar relationship to Lacan’s. In the North and South, we have symmetry of constancy. In the East and West, we have symmetry of alternation. And in-between the coordinates, we have dissymmetry.

⁠

This new encoding reveals something interesting about our previous sequence of random tosses and allows us to read the sequence through a sort of primitive language. What is uncovered is a connected chain to any sequence of random tosses.

⁠

⁠

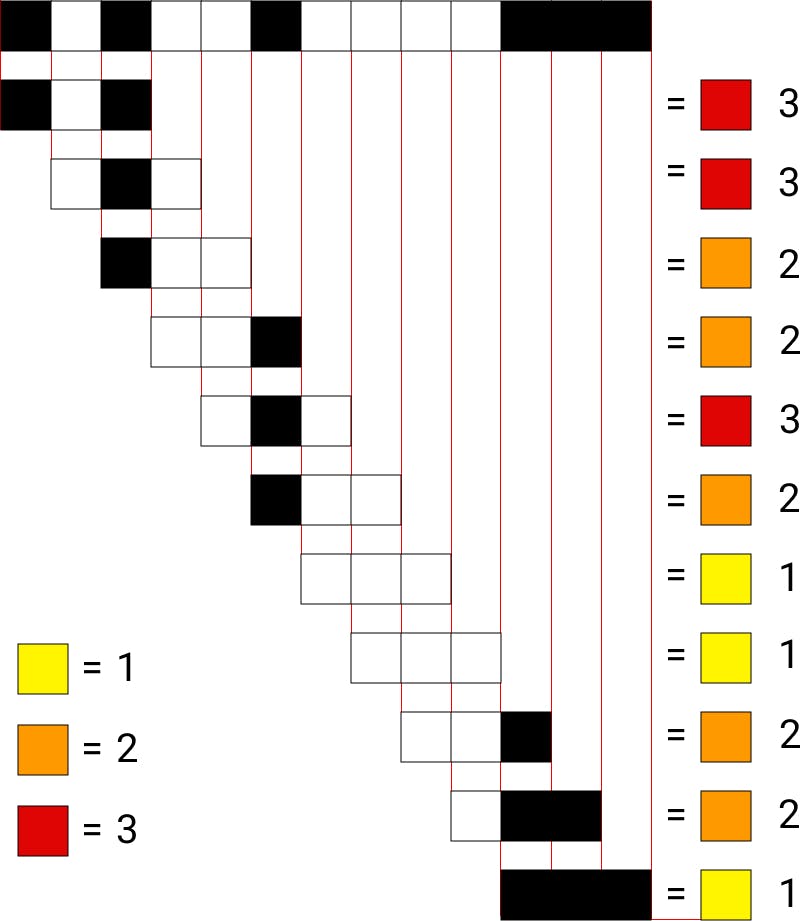
For each cell starting with the 3rd cell, we take its two previous neighbors and determine a corresponding type for the combination. In the case of the first sequence [ H T H ], the patter displays alternating symmetry, or a Type 3 combination. This corresponds to a red block in our diagram. For the next flip, we take its two previous neighbors and perform the same operation. The 4th cell and its 2 previous neighbors [ T H T ] also display alternating symmetry, or a Type 3 combination. This corresponds to a second red block in our diagram. Note that there are some overlapping cells between the first two combinations. We repeat the same pattern until we run out of flips.

⁠

⁠

Here lies the beauty of Lacan’s algorithm. The next flip in the sequence is theoretically random and undetermined. There is a 50/50 chance that it can either be heads or tails. If the next flip is heads (a black block), the next flip and its two previous neighbors [ H H H ] would result in symmetry of constancy, or a Type 1 combination. This corresponds to a new yellow block in our diagram. However, if the next flip is tails (a white block), the next flip and its two previous neighbors [ H H T ] would result in dissymmetry, or a Type 2 combination. This corresponds to a new orange block in our diagram.

We don’t know the outcome between the two yet, but we do know that a new red block is impossible in the above example. Given that our three latests flips were all heads [ H H H ], no matter the outcome of the next flip, we could never have symmetry of alternation, or a Type 3 Combination. In this case, for symmetry of alternation, or a new red block, to occur, we would first need to introduce dissymmetry or a Type 2 combination. This corresponds to a new orange block in our diagram before we ever get to see another red block again. For example, we could go from symmetry of constancy [ H H H ] to dissymmetry [ H H T ] and finally to symmetry of alternation [ H T H ].

What is the significance of this?

1. The sequence of seemingly random tosses are now a linked chain. To demonstrate this relationship, the color coding between the three types of combinations represent temperature in low, medium, and high stages as yellow, orange, and red blocks. Before a temperature goes from low to high, it must pass through a medium stage, and vis versa. Or before a block goes from a yellow to a red block, it must pass through an orange block, and vis versa. You will never see a jump between a Type 1 and Type 3 combination; there will always be a Type 2 combination to bridge the two.

2. The chain exhibits both random and deterministic behavior. We don’t know the next flip and its neighboring combination, but the encoding will necessarily be limited by two options, always leaving a third out. The result is random behavior that exhibits some sense of chaos and order. In the above example, the next block is between heads and tails, or a new yellow or orange block. The choice between the two is random, but the exclusion of a red block option is what allows the pattern to create a smooth connection with previous cells. Regardless of the flip or which next block is chosen between yellow or orange, either choice would blend with the current yellow block. This has some interesting applications for generative art, randomness in generative systems, and the use of color palettes in computer graphics.

3. The chain exhibits a memory. Given that our three latests flips were all heads [ H H H ], we begin with symmetry of constancy. If the next flip is tails [ H H T ], the chain will display a Type 2 combination or dissymmetry. In order for the chain to return to symmetry of constancy, or a Type 1 combination, the chain must first go through a second stage of dissymmetry, or a second Type 2 combination. This is also the case when we start from symmetry of alternation [ H T H ], or a Type 3 combination, and go into dissymmetry [ T H H ], or a Type 2 combination. In this case, we will also need to revisit a second Type 2 combination to make our way back to symmetry of alternation, or a Type 3 combination.

⁠

⁠

The above circuit displays this relationship. If you start with symmetry of constancy [ H H H ], or a Type 1 combination, we could keep flipping heads and remain in an infinite loop of Type 1 combinations. This would correspond to a continuous set of yellow blocks. Note that this is also possible for symmetry of alteration [ H T H ], or a Type 3 combination. If we keep flipping alternating heads/tails, the chain could remain in an infinite loop of symmetry of alternation, or Type 3 combinations. This would correspond to a continuous set of red blocks.

Going back to symmetry of constancy [ H H H ], or a Type 1 combination, if our next flip is tails [ H H T ] the chain exits the loop of Type 1 combinations and moves towards dissymmetry, or a Type 2 combination. This also highlights that there are only ever two choices in any given state. Either the chain remains in a loop of symmetry of constancy, or the chain moves towards dissymmetry. Symmetry of alternation, or a Type 3 combination, is not an option in this case. However, the choice between the two routs remains random and is determined by the next flip.

If we start from our new position of dissymmetry [ H H T ], or a Type 2 combination, we get slightly different rules. The next flip could be heads, which would result in symmetry of alternation [ H T H ], or a Type 3 combination. However, if the next flip is tails, this would display dissymmetry [ H T T ], or a second Type 2 combination. In this case, regardless of the coin flip, symmetry of constancy, or a Type 1 combination, is impossible. The chain going from dissymmetry to symmetry of alternation or from dissymmetry to a second stage of dissymmetry is completely random and determined by the toss, but we can exclude a Type 3 combination from our chain of possibilities. What this means is that once the chain exits out of symmetry into dissymmetry, the chain will have to revisit a second stage of dissymmetry to return back to its original stage of symmetry.

Finally, to address memory more specifically: In our above example, we noted that from our new position of dissymmetry [ H H T ] we have a choice between entering symmetry of alternation [ H T H ] or a second stage of dissymmetry [ H T T ]. If our next flip is heads [ H T H ] and we continue flipping alternating tosses, we would move into symmetry of alternation and continue in an infinite loop of Type 3 combination. However, if the chain ever wants to go back to symmetry of constancy [ H H H ], or a Type 1 combination, the chain will have to revisit dissymmetry, or a Type 2 combination. In this sense, the chain “remembers”, keeps track of its movement, and excludes certain options from possibility. For example:

⁠

⁠

We could start with symmetry of constancy [ H H H ], Type 1 combination

Flip tails and move to dissymmetry [ H H T ], Type 2 combination

Flip heads and move to symmetry of alternation [ H T H ], Type 3 combination

Retain an alternating loop of heads and tails for 100 flips, Type 3 combinations

Break the alternating loop with two heads in a row [ T H H ], second Type 2 combination

And finish with a third heads returning to symmetry of constancy [ H H H ], second Type 1 combination

Once you exit out of a type of symmetry into dissymmetry, the chain will have to revisit a second stage of dissymmetry to go back to its original stage of symmetry, regardless of the length of the chain or amount of tosses. For Lacan, this is significant because it speaks to a form of memory that can exists without the need for a thinking subject and largely influences his views on how the unconscious operates. “The unconscious cannot forget, composed of "letters" working, as they do, in an autonomous, automatic way; it preserves in the present what has affected it in the past, eternally holding on to each and every element, remaining forever marked by all of them” (Fink 1995, p. 20)

4. The chain operates through a process of symbolic exclusion. At every step of the chain, the next random toss results in either of two types of combinations, but a third is always excluded. If we start with symmetry of constancy [ H H H ], the next flip could be heads and maintain symmetry of constancy [ H H H ] or be tails and break into dissymmetry [ H H T ]. But symmetry of alternation is impossible. You can continue to follow the chain and this pattern will continue to repeat. Lacan wants to say that this process of exclusion is not merely accidental and is what allows the chain of possibilities to exists in the first place. The two possibilities for the next flip and their corresponding block color make sense in part because the third possibility, deriving symmetry of alteration after symmetry of constancy or a red block after a yellow block, has been excluded from the chain of possibilities in the example above. This will influence his general views on language as a symbolic structure, his theories on lack, and his distinctions between the Symbolic, the Imaginary, and The Real.

Fractal Memory - Cellular Automata (FMCA)

“It’s not what happens afterwards which is modified, but everything which went before. We have a retroactive effect—nachträglich, as Freud calls it—specific to the structure of symbolic memory, in other words to the structure of remembering (Lacan 1955, p. 185)

⁠

This article assumes the reader has a basic understanding of Cellular Automata and is meant more for generative artists interested in implementing Lacan’s algorithm. A full explanation of CA would exceed the scope of this article.

CA describes a computational model or algorithm often used in generative art. We will be focusing on 2D Cellular Automata, which sees a canvas as a grid of cells. Each cell is either on or off and represented by 0s or 1s. Each cell in the grid has a set of neighbors, and we can determine a set of rules to decided whether a cell lives or dies depending on its current state and its neighbors. Once all new states for each cell in the grid have been calculated, a new grid is formed, and the same rules are applied. In the above example, we zoom into a single cell on a grid and its immediate neighbors. We see that the cell in the center goes from 1 - 0 - 1 - 1 as to simulate the changes of the cell according to its neighbors in each grid. The actual rules that are applied to determined whether a cell lives or dies according to its neighbors are not the focus of this article. There are countless implementations of these rules, and we will discuss some approaches below.

However, once you are able to generate a basic CA model, you will notice that each cell on the grid has a history of being on and off, or a history 0s and 1s. For each cell on the grid, we can keep track of its previous states and reformulate Lacan’s algorithm to determine the current state of the cell in Lacan’s chain. Note that Lacan’s chain begins on the third flip, due to the need of two previous neighbors.

⁠

⁠

Two significant changes to classical CA.

This is a new model to achieve a CA with 3 states while staying true to the original concept of CA. The underlying grid that determines whether a cell lives or dies is still an elementary process of on/off or 0s and 1s. We are not flipping between a 3 sided coin. However, the sequence of a states history is able to display the 3 unique states internal to the structure of the random set of flips. The input for the algorithm is the next flip, on/off, but the output and display generates much more interesting patterns and connections.

The CA could be described as “spatiotemporal” in that its display is impacted not only by the neighboring cells around and individual cell, which determine whether that cell lives or dies, but also its history of being on/off, which determines its sequences in Lacan’s chain and eventual display. Both the cells position within the grid and its history effect the outcome of the display.

Finally, I see CA as a powerful model to explore Lacan’s notion of apres-coup further. This idea that the symbolic chain records its history internal to its structure and has retroactive effects in terms of what its future looks like is manifested in these models.

Multiple Neighborhood Cellular Automata (MNCA)

One quick note on Multiple Neighborhood Cellular Automata (MNCA). So far, I have not layed out a set of rules to describe how we should determine whether an individual cell lives or dies. I have only discussed what we should do once we have a working cellular automata with a grid of cells containing a history of 0s and 1s.

So far, I have found interesting results when combining Lacan’s algorithm with MNCA principles. All credit goes to Slackermanz who innovated this method.

⁠

Instead of determining a cell’s life based on a singular and immediate neighborhood, we can think of a cell as having multiple neighborhoods. In the above diagram, the orange cells display 3 groups of distinct neighborhoods. This allows us to get more creative with how we determine what a neighborhood looks like, the quantity of neighborhoods, and the rules to determine whether a cell lives or dies based on these neighborhoods.

One contribution I’d like to add to this topic deals with reutilizing Lacan’s encoding to determine whether a cell lives or dies according to its neighborhoods. For example, if you begin with 3 neighborhoods, you could think of each as part of a sequence [ 1 1 1 ] representing 3 live neighborhoods. This gives us symmetry by constancy which we can represent as 1. In contrast, we could have a sequence of [ 1 1 0 ] representing 2 live neighborhoods and 1 dead neighborhood. This gives us dissymmetry which we could represent as 0. Note that at this level, we are merely determining whether a cell lives or dies, a binary operation. This means we don’t want to create a 3 level encoding and instead should group both types of symmetry (constancy and alternation) as 1. You could determine a set of rules to evaluate the life/death of each individual neighborhood, but the overall encoding simply looks at the sequence of the neighborhoods combined to determine the next cell.

Closing Thoughts

It is worth noting that this is an incomplete exploration of Lacan’s teachings on cybernetics. This article covers the first half of Lacan’s exercises in his seminar on The Purloined Letter. Further exercises reveal a second encoding scheme built on top of the original encoding of 1-2-3 Type combinations. (Brahnam 2018, p. 208)

Additionally, in the same way that MNCA revolutionized CA by introducing the concept of multiple neighborhoods, Lacan’s further encodings could be adapted to pool information from multiple sources of “memory” to determine its display.

References

Brahnam, Sheryl. (2018). Primordia of après-coup, fractal memory, and hidden letters: Working the exercises in Lacan's seminar on "The Purloined Letter".

Fink, Bruce. (1995). The Lacanian subject: Between language and jouissance. Princeton University Press.

Lacan, Jacques (1955) Odd or Even? Beyond Intersubjectivity. The Seminar of Jacques Lacan: Book 2: The Ego in Freud’s Theory and in the Technique of Psychoanalysis 1954-1955. Edited by Jacques-Alain Miller. 175-190. Cambridge University Press.

Lacan, Jacques (1955) Psychoanalysis and Cybernetics, or on the Nature of Language. The Seminar of Jacques Lacan: Book 2: The Ego in Freud’s Theory and in the Technique of Psychoanalysis 1954-1955. Edited by Jacques-Alain Miller. 294-308. Cambridge University Press.

Lacan, Jacques. (2007) The Purloined Letter. Ecrits. 6-50. Translated by Bruce Fink, WW Norton.

Liu, Lydia H. (2010). The Cybernetic Unconscious: Rethinking Lacan, Poe, and French Theory. Critical Inquiry. 36. 288-320. 10.1086/648527.

Want to print your doc?
This is not the way.

Try clicking the ⋯ next to your doc name or using a keyboard shortcut (

CtrlP

) instead.